Generators¶
VoxelGenerator allows to generate voxels given a specific area in space, or from a single position. They can serve as a base to automate the creation of large landscapes, or can be used in a game to generate worlds. They have an important place because storing voxel data is expensive, while procedural sources are lightweight.
How generators work¶
Generators currently run on the CPU and primarily work on blocks of voxels. For example, given a VoxelBuffer of 16x16x16 voxels, they decide what value each one will take. Using blocks makes it easier to split the work across multiple threads, and focus only on the area the player is located, especially if the world is infinite.
Voxel data is split into various channels, so depending on the kind of volume to generate, one or more different channels will be used. For example, a Minecraft generator will likely use the TYPE channel for voxel types, while a smooth terrain generator will use the SDF channel to fill in distance field values.
Generators have a thread-safe API. The same generator generate_block method may be used by multiple threads at once. However, depending on the class, some parameters might only be modifiable from the main thread, so check the documentation to be sure.
If a volume is not given a generator, blocks will be filled with air by default.
Basic generators¶
The module provides several built-in generators. They are simple examples to get a quick result, and showing how the base API can be implemented (see source code).
Some of these generators have an option to choose which channel they will work on. If you use a smooth mesher, use the SDF channel (1), otherwise use the TYPE channel (0).
The following screenshots use a smooth VoxelLodTerrain.
Flat¶
Generates a flat ground.
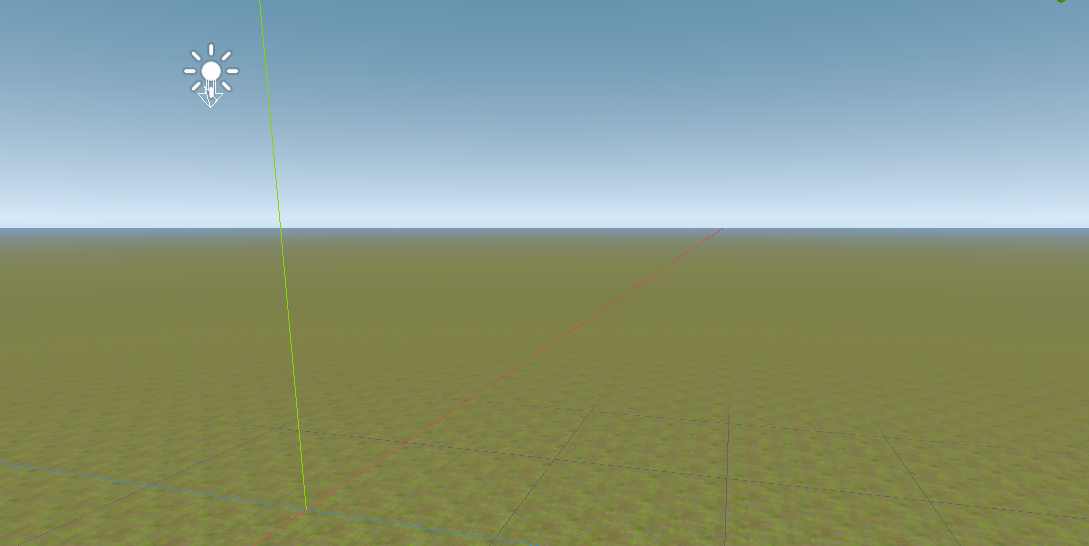
Waves¶
Generates waves.
Image¶
Generates a heightmap based on an image, repeated infinitely.

Note
With this generator, an Image resource is required. By default, Godot imports image files as StreamTexture. You may change this in the Import dock. At time of writing, in Godot 3, this requires an editor restart.
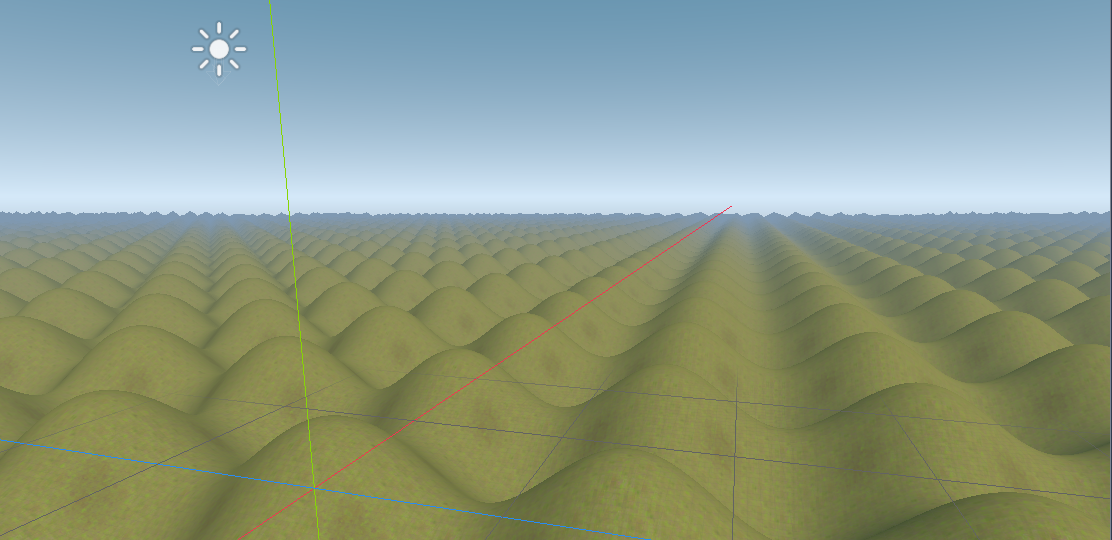
Noise2D¶
Generates a heightmap based on fractal noise.
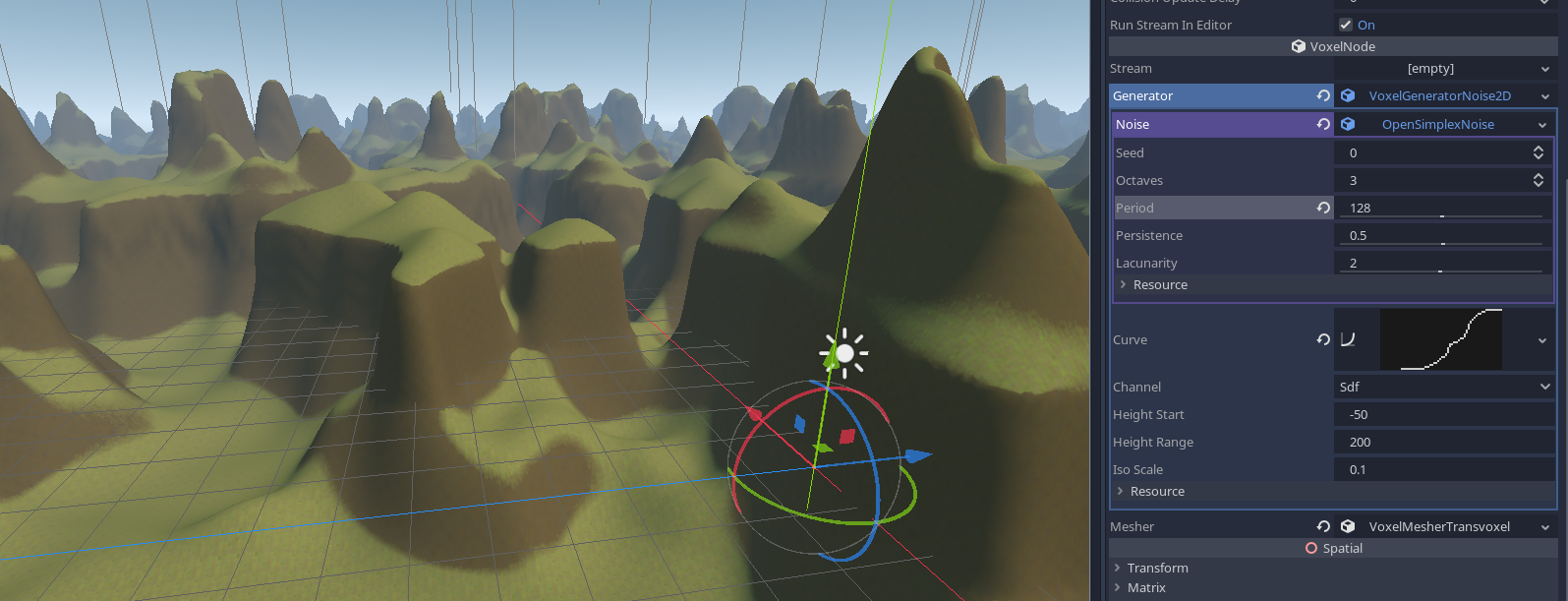
Noise (3D)¶
Generates a blobby terrain with overhangs using 3D fractal noise. A gradient is applied along height so the volume becomes air when going up, and closes down into matter when going down.

Node-graph generators with VoxelGeneratorGraph¶
Basic generators may often not be suited to make a whole game from, but you don't necessarily need to program one. C++ is a very fast language to program a generator but it can be a tedious workflow, especially when prototyping. If you need smooth terrain, a graph-based generator is available, which offers a very customizable approach to make procedural volumes.
Warning
This generator was originally made for smooth terrain, but works with blocky too, to some extent.
Concept¶
Voxel graphs allow to represent a 3D density by connecting operation nodes together. It takes 3D coordinates (X, Y, Z), and computes the value of every voxel from them. For example it can do a simple 2D or 3D noise, which can be scaled, deformed, masked using other noises, curves or even images.
A big inspiration of this approach comes again from sculpting of signed-distance-fields (every voxel stores the distance to the nearest surface), which is why the main output node may be an SdfOutput. A bunch of nodes are meant to work on SDF as well. However, it is not strictly necessary to respect perfect distances, as long as the result looks correct for a game, so most of the time it's easier to work with approximations.
Note
Voxel graphs are half-way between programming 3D shaders and procedural design. It has similar speed to C++ generators but has only basic instructions, so there are some maths involved. This might get eased a bit in the future when more high-level nodes are added.
Examples¶
Flat plane¶
The simplest possible graph with a visible output is a flat plane. The SDF of a flat plane is the distance to sea-level (0), which is sdf = y. In other words, the surface appears where voxel values are crossing zero.
Right-click the background of the graph, choose the nodes InputY and SdfOutput, then connect them together by dragging their ports together.
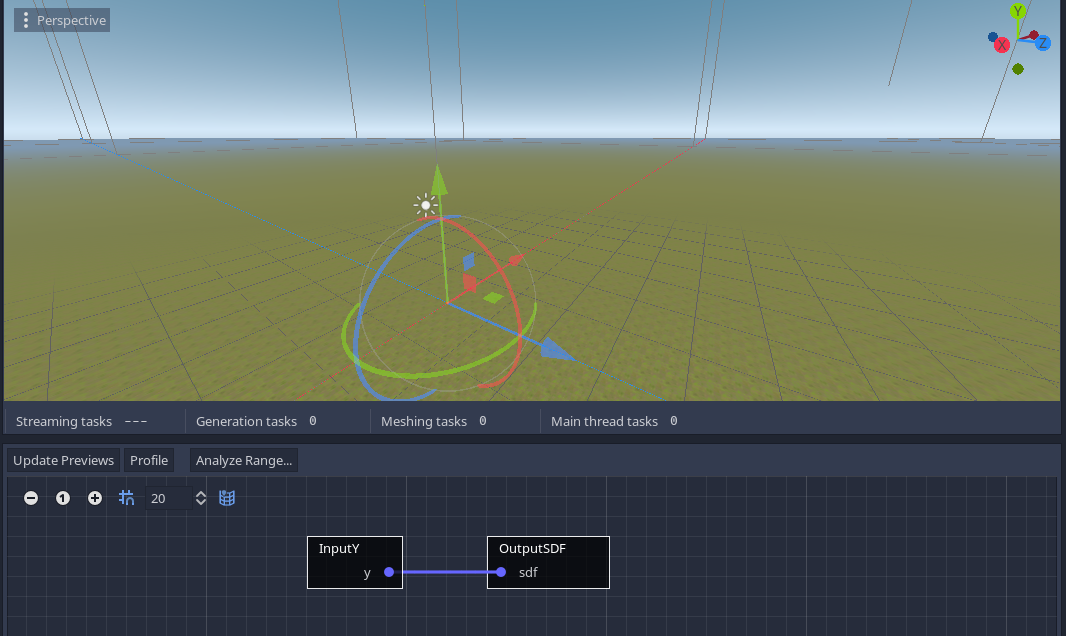
It is possible to decide the height of the plane by subtracting a constant (sdf = y - height), so that sdf == 0 will occur at a higher coordinate. To do this, an extra node must be added:
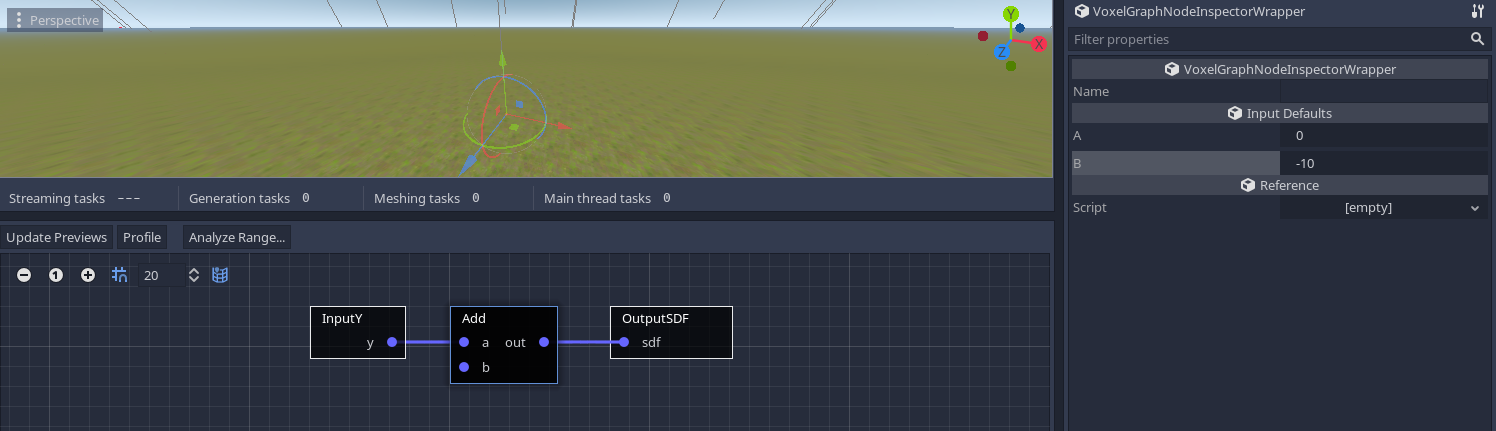
By default, the Add node does nothing because its b port is not connected to anything. It is possible to give a default value to such port. You can set it by clicking on the node and changing it in the inspector.
(note: I used Add with a negative value for b, but you can also use a Subtract node to get the same result).
Noise¶
A flat plane is simple but a bit boring, so one typical way to generate a terrain is adding good old fractal noise. You can do this in 2D (heightmap) or 3D (volumetric).
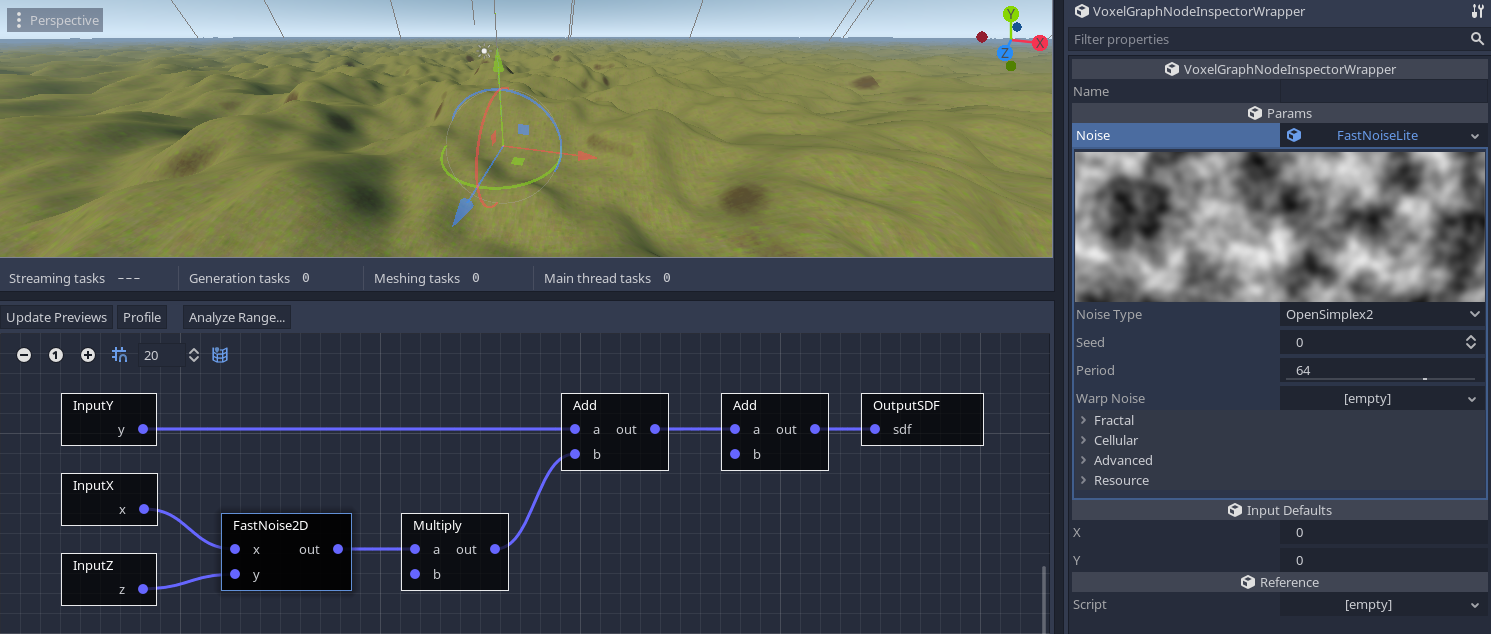
The 2D approach is simpler, as we only need to take our previous setup, and add 2D noise to the result. Also, since noise is generated in the range [-1 to 1], we also need a multiplier to make it larger (sdf = y - height + noise2d(x, y) * noise_multiplier).
There are several types of noise available, each with their own parameters. At time of writing, FastNoise2D noise is the best option. Noise2D works too but it is slower and more limited (it uses Godot's OpenSimplexNoise class).
Note
After you create this node, a new FastNoiseLite resource must be created in its parameters. If that resource is not setup, an error will occur and no voxels will be generated.
3D noise is more expensive to compute, but is interesting because it actually produces overhangs or even small caves. It is possible to replace 2D noise with 3D noise in the previous setup:
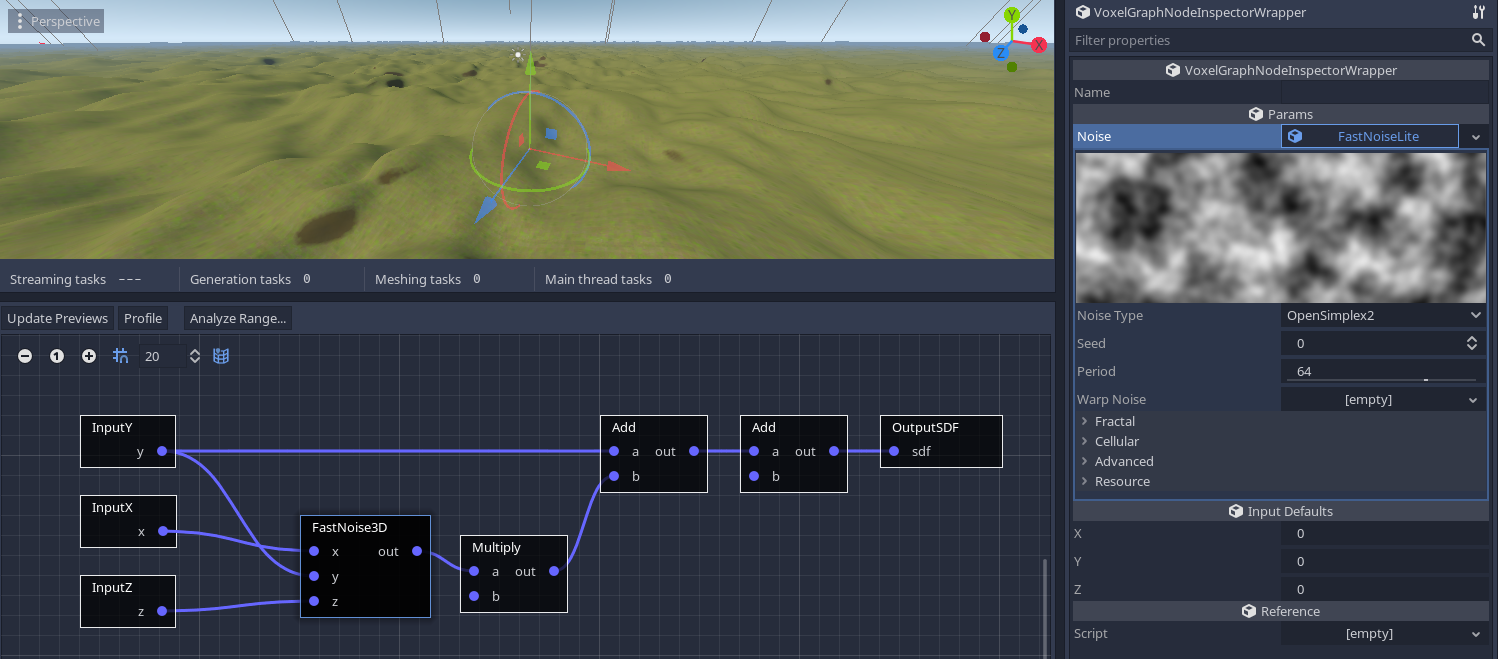
You might notice that despite it being 3D, it still appears to produce a heightmap. That's because the addition of Y in the graph is gradually offsetting noise values towards higher and higher values when going towards the sky, which makes the surface fade away quickly. So if we multiply Y with a small value, it will increase slower, letting the 3D noise expand more (sdf = y * height_multiplier - height + noise3d(x, y, z)):
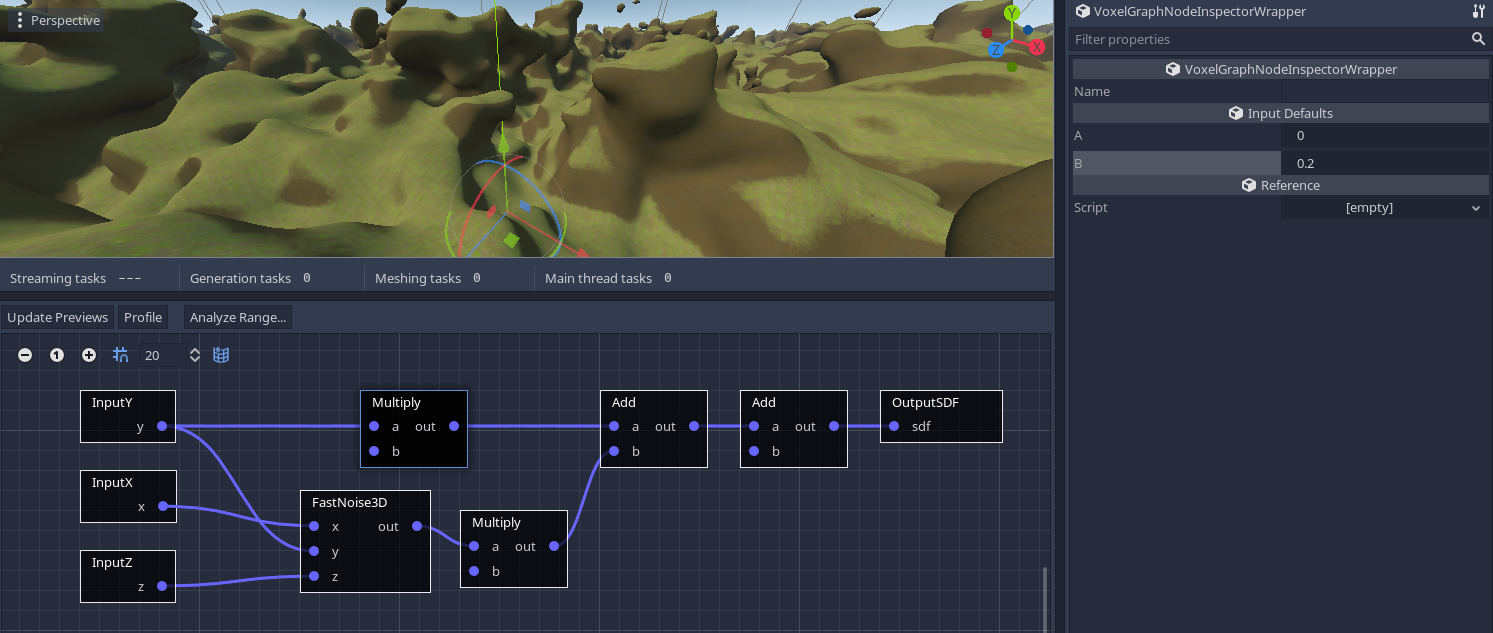
Note
Some nodes have default connections. For example, with 3D noise, if you don't connect inputs, they will automatically assume (X,Y,Z) voxel position by default. If you need a specific constant in an input, this behavior can be opted out by turning off autoconnect_default_inputs in the inspector.
Planet¶
We are not actually forced to keep generating the world like a plane. We can go even crazier, and do planets. A good way to begin a planet is to make a sphere with the SdfSphere node:
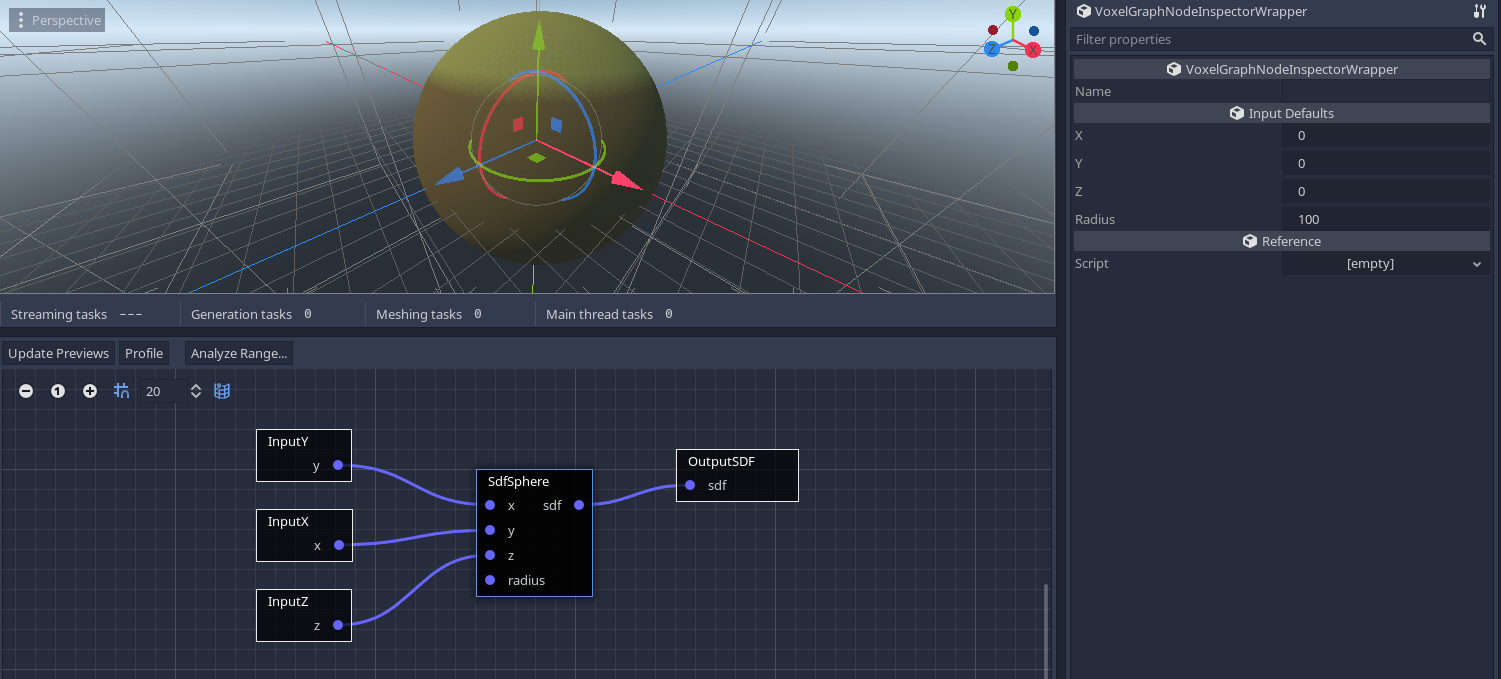
We cannot really use 2D noise here, so we can add 3D noise as well:
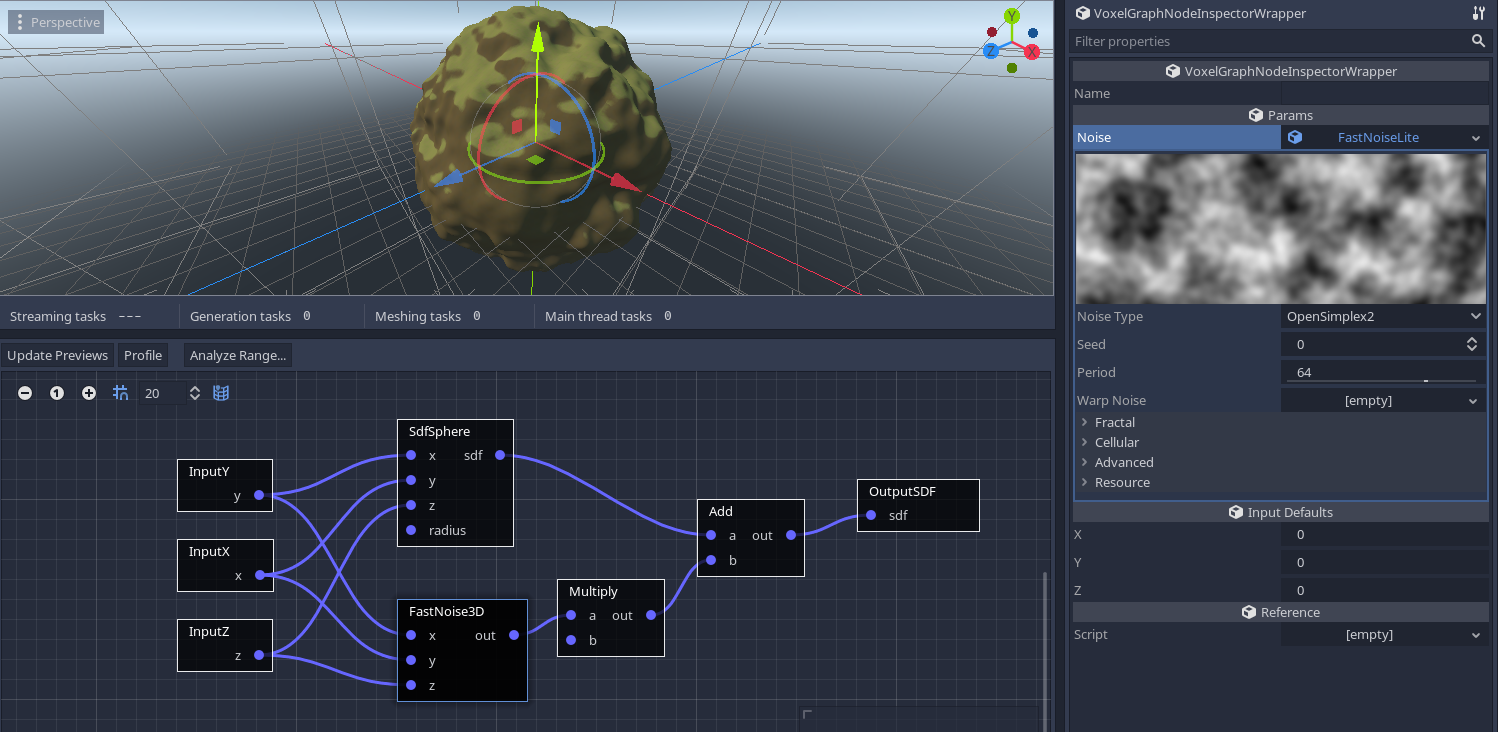
However you might still want a heightmap-like result. One way to do this is to feed the 3D noise normalized coordinates, instead of global ones. Picking a ridged fractal can also give an eroded look, although it requires to negate the noise multiplier node to invert its distance field (if we leave it positive it will look puffed instead of eroded).
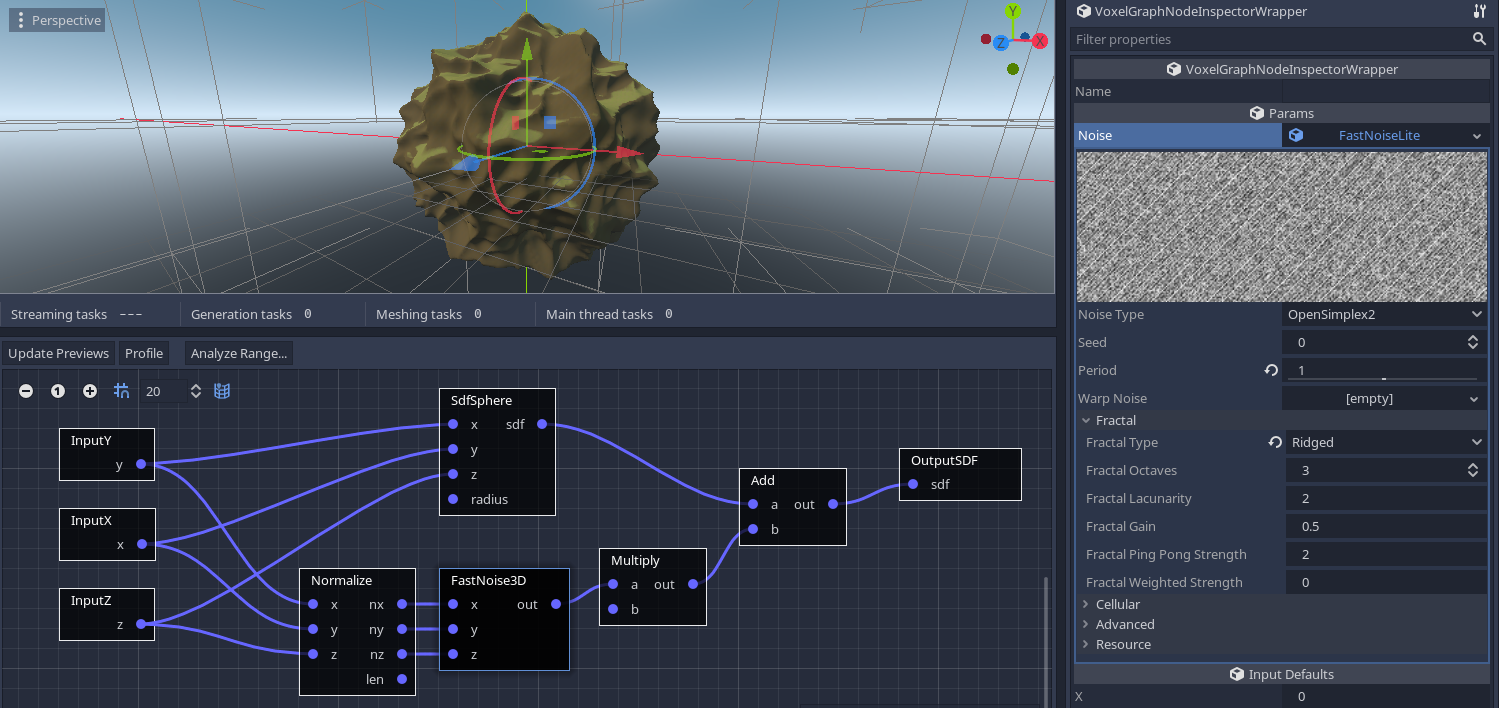
Note
You can obtain a donut-shaped planet if you replace the SdfSphere node with a SdfTorus node.
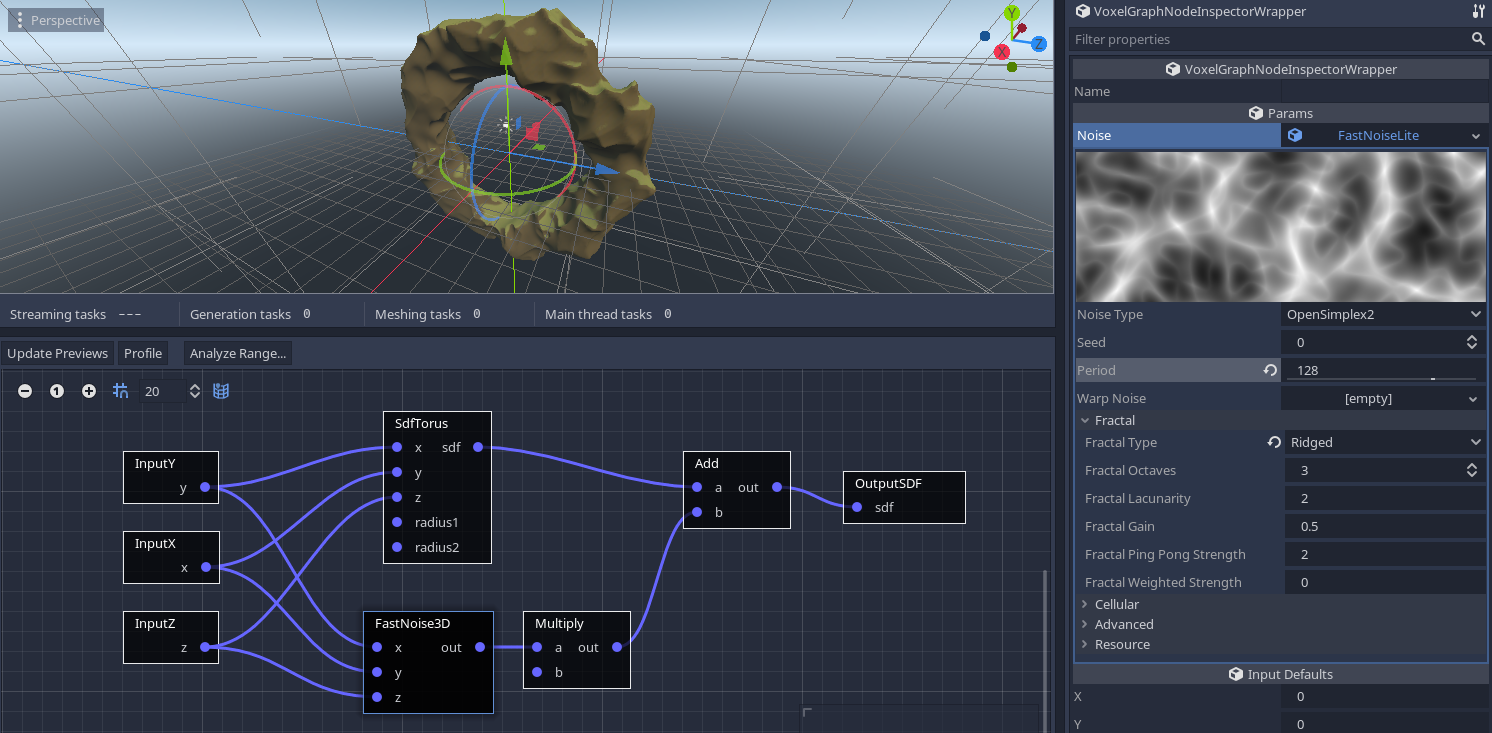
More techniques can be found in the Procedural Generation section.
Usage with blocky voxels¶
It is possible to use this generator with VoxelMesherBlocky by using an OutputType node instead of OutputSDF. However, VoxelMesherBlocky expects voxels to be IDs, not SDF values.
The simplest example is to pick any existing SDF generator, and replace OutputSDF with a Select node connected to an OutputType. The idea is to choose between the ID of two different voxel types (like air or stone) if the SDF value is above or below a threshold.
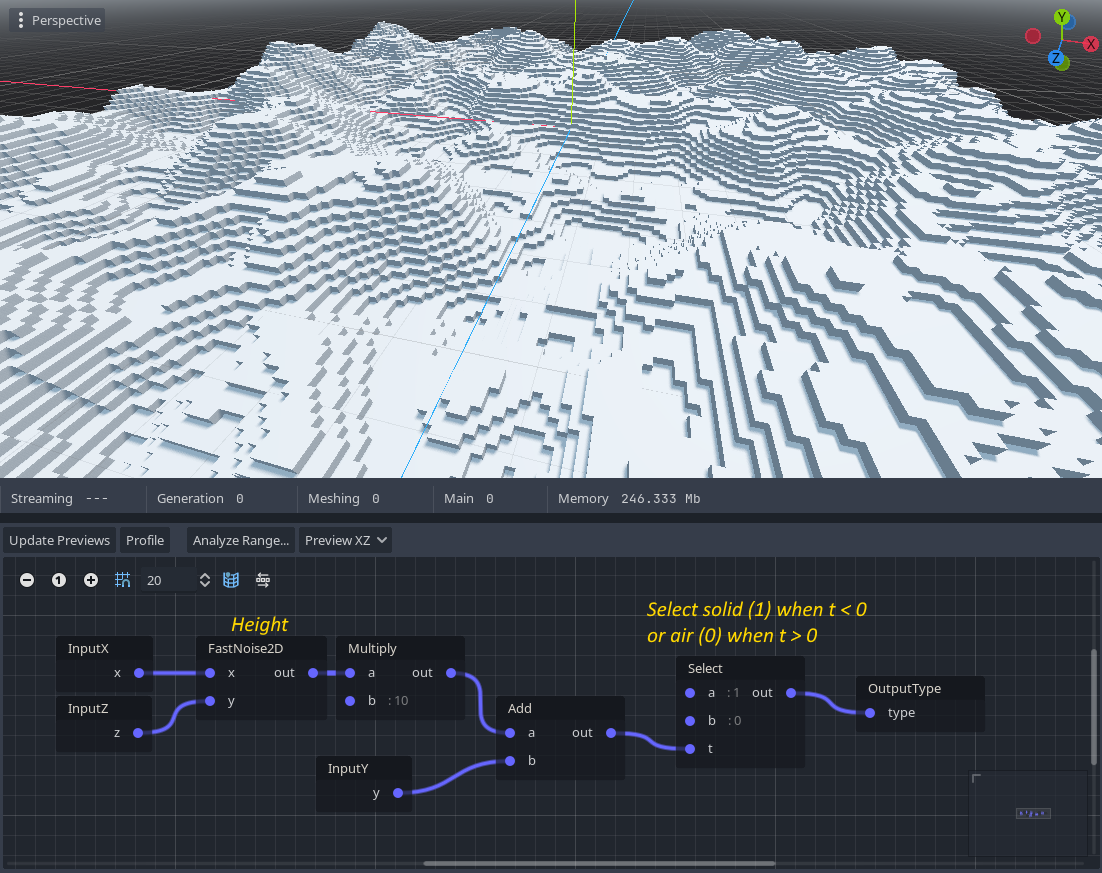
If more variety is needed, Select nodes can be chained to combine multiple layers, using different thresholds and sources.
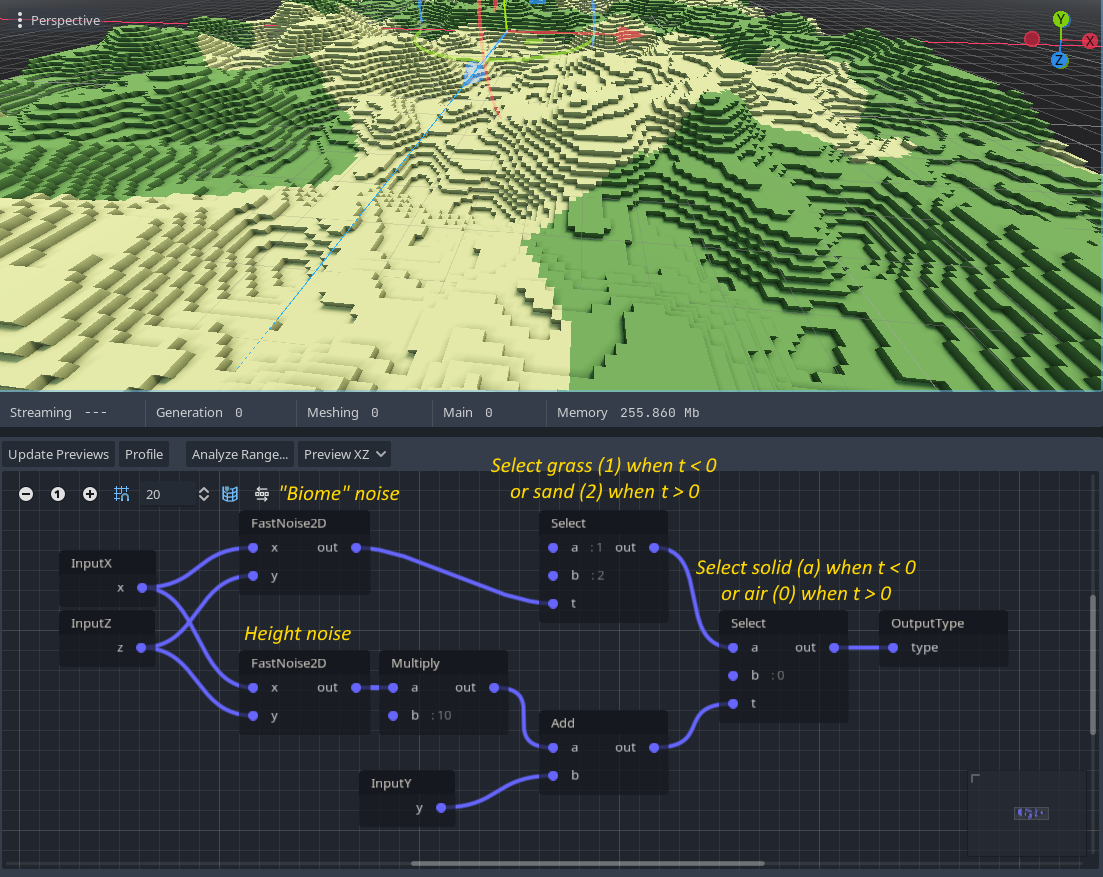
Select creates a "cut" between the two possible values, and it may be desirable to have some sort of transition. While this isn't possible with VoxelMesherBlocky without a lot of different types for each value of the gradient (usually done with a shader), it is however easy to add a bit of noise to the threshold. This reproduces a similar "dithered" transition, as can be seen in Minecraft between sand and dirt.
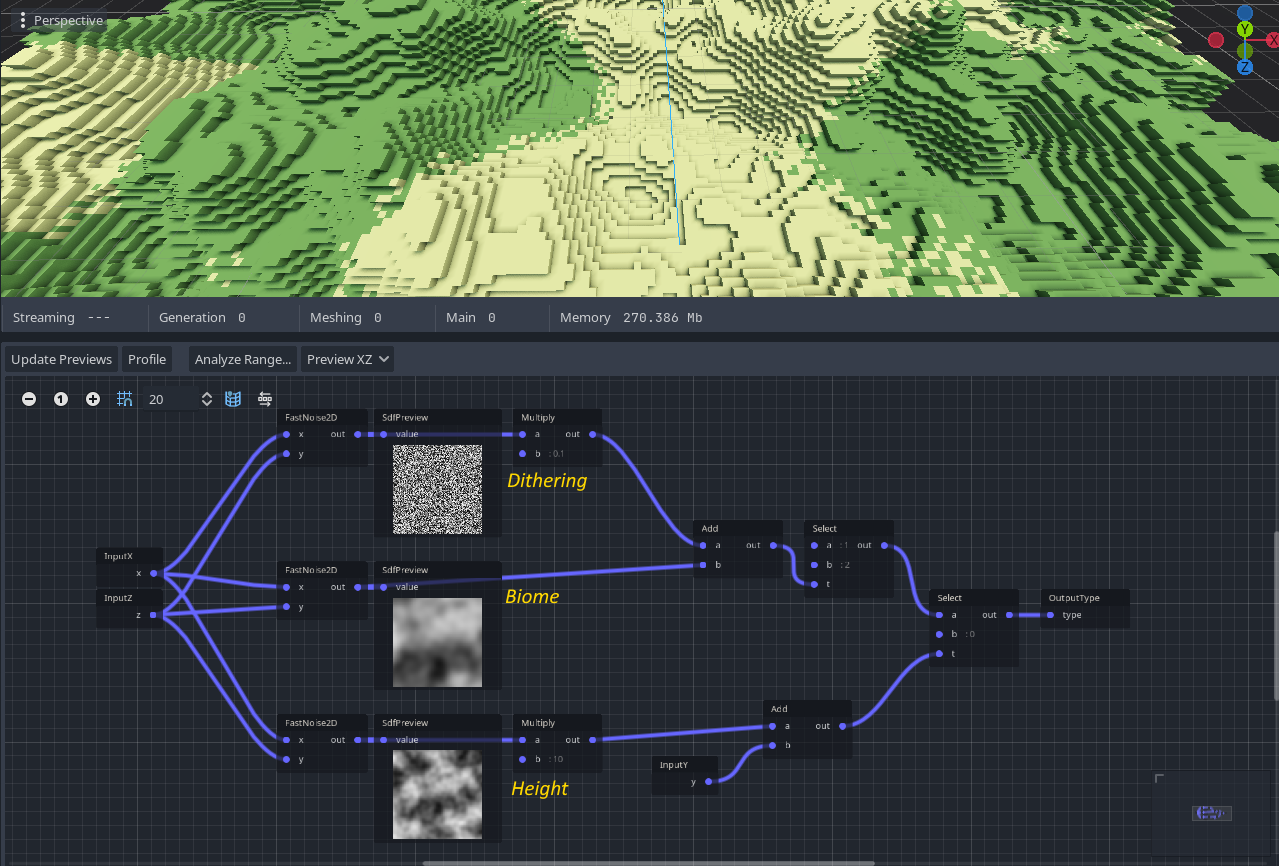
Currently, graph generators only work per voxel. That makes them good to generate base ground and biomes, but it isn't practical to generate structures like trees or villages with it. This may be easier to accomplish using a second pass on the whole block instead, using a custom generator.
Relays¶
A special Relay node exists to organize long connections between nodes. They do nothing on their own, they just redirect a connection. It also remains possible for a relay to have multiple destinations.
Preview nodes¶
It is possible to preview the output of nodes with the SdfPreview node. This node will display a slice of the 3D data as a greyscale image, or a colored image depending on its settings. This is useful to check if a branch is outputting expected values.
Note
- Preview nodes will only work if the output they are connected to is also connected to an actual output of the graph.
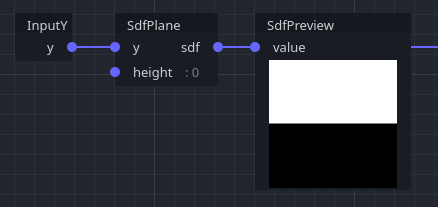
In the example above, the preview shows the output of a SdfPlane node. Values are negative below the surface, positive above the surface, and increase gradually along the Y axis. As a result, previews show white above, and black below.
By default, the node shows a slice along the XY plane, but you can change it to the XZ plane in case you need a top-down view, in the Debug -> Preview Axes menu on top of the editor.
Here is the output for a sphere of radius 50:
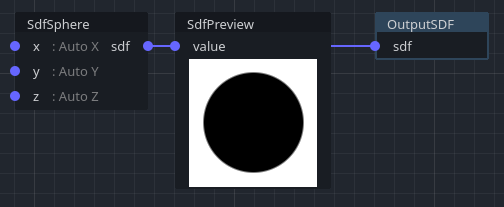
By default, each pixel of the preview corresponds to 1 unit of space. You can zoom by holding the CTRL key and using the mouse wheel on top of the preview. You can also move around by holding CTRL and dragging the preview's viewport holding the middle mouse button.
Pan & zoom locations can be reset to defaults by using the menu Debug -> Preview Axes -> Reset Location.
Previews show black and white based on a specific range defined in their properties. By default, -1 is black, 1 is white (so 0 is actually grey). You can change that range by selecting the preview node and using the inspector.
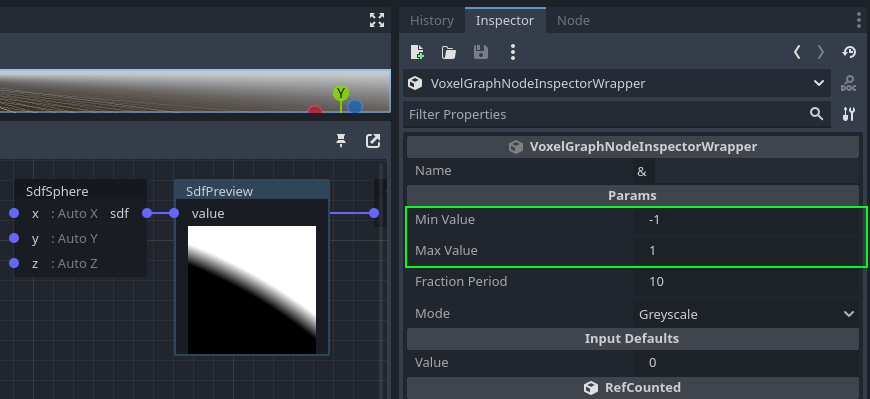
When working with signed distance fields (SDF), preview nodes can also display values in a more specialized way. In the inspector, you can change the mode to SDF:
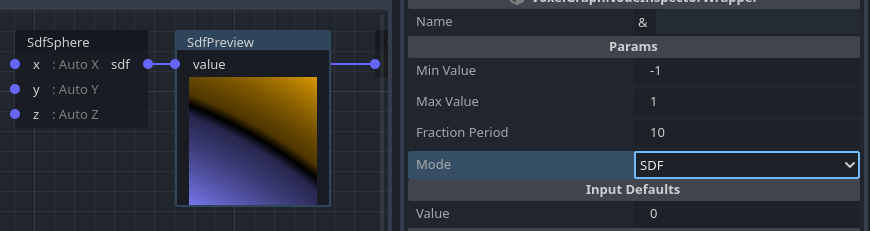
This mode shows negative values as blue (inside shape) and positive values as yellow (outside shape).
It also renders "bands" of repeating gradients to better visualize how they propagate away from the surface. The length of those bands is controlled by fraction period.
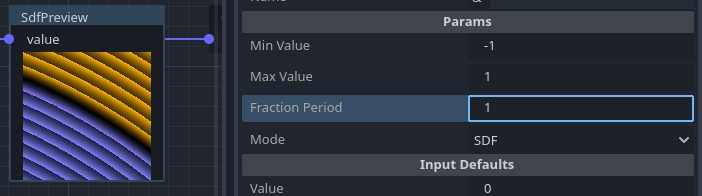
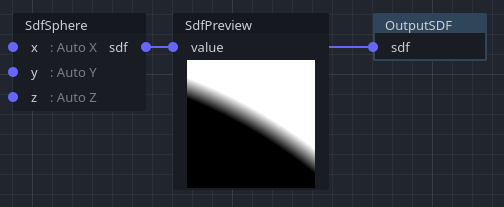
With a sphere, gradients are quite regular, which is usually best. But when using noise as signed distance field, you can notice how gradients actually evolve below and above the surface:
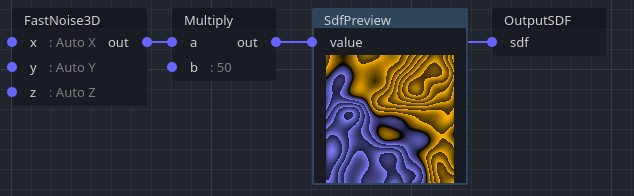
Noise is a lot more inconsistent. However, most of the time, this isn't a big deal. It depends on what operations you do with the terrain. If the "speed" of gradients varies too sharply, especially near the surface, it can be the cause of precision loss or blockyness in generated meshes. It can also be a problem when approximating the surface solely from SDF voxels or using sphere tracing.
Custom generator¶
See Scripting
Using VoxelGeneratorGraph as a brush¶
This feature is currently only supported in VoxelLodTerrain and smooth voxels.
VoxelTool offers simple functions to modify smooth terrain with do_sphere for example, but it is also possible to define procedural custom brushes using VoxelGeneratorGraph. The same workflow applies to making such a graph, except it can accept an InputSDF node, so the signed distance field can be modified, not just generated.
Example of additive do_sphere recreated with a graph:
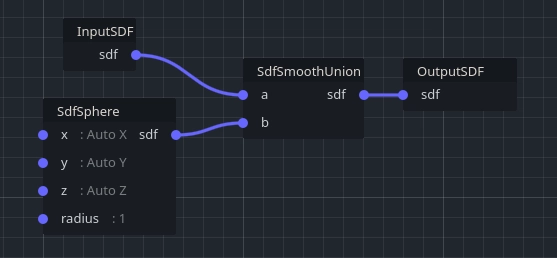
A more complex flattening brush, which both subtracts matter in a sphere and adds matter in a hemisphere to form a ledge (here defaulting to a radius of 30 for better preview, but making unit-sized brushes may be easier to re-use):
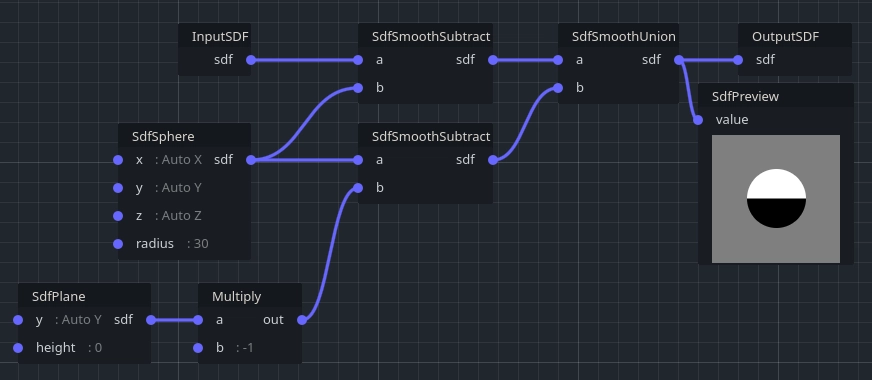
One more detail to consider, is how big the original brush is. Usually voxel generators have no particular bounds, but it matters here because it will be used locally. For example if your make a spherical brush, you might use a SdfSphere node with radius 1. Then, your original size will be (2,2,2). You can then transform that brush (scale, rotate...) when using do_graph at the desired position.
Re-usable graphs with VoxelGraphFunction¶
VoxelGraphFunction allows to create graphs that can be used inside other graphs. This is a convenient way to re-use and share graphs.
Creating a function¶
A VoxelGraphFunction can be created in the inspector and edited just like a VoxelGeneratorGraph, except it will lack some features only found on the latter. It is recommended to save functions as their own .tres files, because this is what allows to pick them up in other graphs.
Note
A VoxelGraphFunction cannot contain itself, directly or indirectly. Doing this will result in Godot failing to load it.
Exposing inputs and outputs¶
To be usable in other graphs, functions should have inputs and outputs. Inputs can be added to the function by creating nodes InputX, InputY, InputZ, InputSDF or CustomInput. Outputs can be added by creating nodes OutputX, OutputY, OutputZ, CustomOutput etc.
Non-custom inputs and outputs such as InputX or OutputX are special nodes, and are identified by their type. They are recognized by the engine for specific purposes. You can have multiple nodes with the same type, but they will always refer to the same input of the function.
Custom inputs and outputs are identified by their name. If you add 2 CustomInput nodes and give them the same name, they will get their data from the same input. It is recommended to give a name to custom input and output nodes. Empty names still count as a name (so multiple CustomInput without names will refer to the same unnamed input).
Exposing parameters¶
Currently parameters cannot be exposed, but it is planned.
Handling changes¶
When an existing function changes (new/removed inputs/outputs for example), it is possible that other graphs using it will break. If you try to open them, some of the nodes and connections could be missing.
Currently, you are expected to fix these graphs, and save them. You can also change the offending function so that its inputs, outputs and parameters are what you expect. However if you save a broken graph, you might loose some connections or nodes.
Debugging¶
Editor tools such as profiling, output previews or range analysis are currently unsupported inside a VoxelGraphFunction. It is also not possible to inspect internal nodes of a function when editing a VoxelGeneratorGraph.
It is planned to have these tools available when editing a standalone VoxelGraphFunction in the future. This will be done by moving features out of VoxelGeneratorGraph so they become more generic.
Inspecting a function "instance" (and sub-instances...) may be desirable, but it is tricky to implement. It could be done as an "Open Inside" feature, to inspect data within the context of the "containing graph". However because functions are fully unpacked and optimized out internally, the engine has to trace back the information to original nodes. Tracing is already present to some degree, but only maps the "top-level" graph to fully-expanded/optimized graph, with no in-between information. This might be worked on further in the future.
VoxelGeneratorGraph nodes¶
A complete list of nodes can be found here.
Multi-pass generation with VoxelGeneratorMultipassCB¶
Sometimes you need to write a custom generator that needs to produce structures made of voxels in the terrain itself overlapping neighbor chunks, such as trees. While it is possible to make trees with a deterministic approach, it has limitations and is a bit harder to understand. Also, you might want to have access to an entire vertical section of the world while generating it, instead of just a 16x16x16 chunk.
Contrary to other generators, VoxelGeneratorMultipassCB allows you to structure generation in several passes, where you can access neighbor chunks. It also works in columns, so you have access to a full vertical section of the world. Things like placing a structure across chunk borders just works.
You may find early design information in this issue.
World model¶
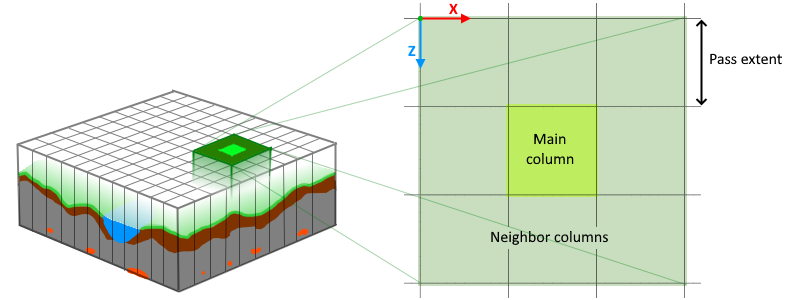
This generator is suffixed "CB" for "Column-Based". The world this generator works on is "flat". Similar to Minecraft, generation occurs within a fixed region going from minimum to maximum altitude (specified with properties), in columns of 16x16 voxels. Then everything above is air, and everything below is either bedrock or just air too. The amount of neighbor columns a pass can access is called the "extent" of the pass.
While the multipass column logic only works within the fixed vertical range, it will be possible to define what's outside of that range, but it has to be single pass.
In sections below, "column" will refer to a stack of blocks within the fixed region.
Note
Fixed column height is a design choice to make the generator simpler to implement, and should cover the majority of terrains. However, this is only a limitation of the generator. VoxelTerrain remains unlimited vertically, so players can still build higher than the area handled by the terrain generator.
API¶
This generator is implemented using a script, similar to VoxelGeneratorScript. The difference is this function:
extends VoxelGeneratorMultipassCB
func _generate_pass(voxel_tool: VoxelToolMultipassGenerator, pass_index: int):
var min_pos := voxel_tool.get_main_area_min()
var max_pos := voxel_tool.get_main_area_max()
if pass_index == 0:
# Base terrain
for gz in range(min_pos.z, max_pos.z):
for gx in range(min_pos.x, max_pos.x):
# Do things with `voxel_tool`
# ...
elif pass_index == 1:
# Trees
# ...
Unlike VoxelGeneratorScript where _generate_block is called once for every 16x16x16 block of the terrain, _generate_pass is called multiple times for every column of blocks, once for every pass. Subsequent calls can access and modify voxels left by previous passes.
Columns may be designated in two different ways in this process:
- "Main" column: this is the column being processed by
_generate_pass. The available area passed withvoxel_toolwill be centered on that column. Usually, if you plant trees, their trunk should only be planted in the main column, to keep results consistent. - "Neighbor" columns: these are around the main column, which also means they will be "seen" by more than one column processing during the same pass.
Note
Accessing neighbors doesn't mean this generator has access to voxels of the terrain players have access to. Internally, the generator has its own separate representation of the world, and only stores blocks that are generating. Columns don't interact with the game, and the game can't interact with them.
Note
Just like VoxelGeneratorScript, run_stream_in_editor will turn off if you have a script attached to the generator. This is because modifying scripts while another thread is running them in the editor can lead to unpredictable behavior and crashes.
Column inter-dependencies¶
Inter-dependency is a core concept that makes this generator different from the others. It is a direct result of the fact each column can access its neighbors while generating. It is intuitive to do so, but it creates side-effects.
"Completing" a pass¶
Let's say we define 2 passes:
- Pass 1: base terrain. Just combinations of Perlin noise and shapes, where it is not necessary to access neighbors.
- Pass 2: trees. They could have various shapes and overlap across chunks, and could check if they fit or of they have access to sunlight. That pass will access up to 1 chunk away.
With just these two passes, generating one final column requires to process a bunch of other columns:
a a a a a a = pass 1 partially affected by b
a b b b a b = pass 2 incomplete, partially affected by itself
a b B b a B = pass 2 complete
a b b b a
a a a a a
The reason is that in order to completely finish Pass 2 on a specific column, we can't just run it once on that column. We must also do it on all neighbors that can reach that column.
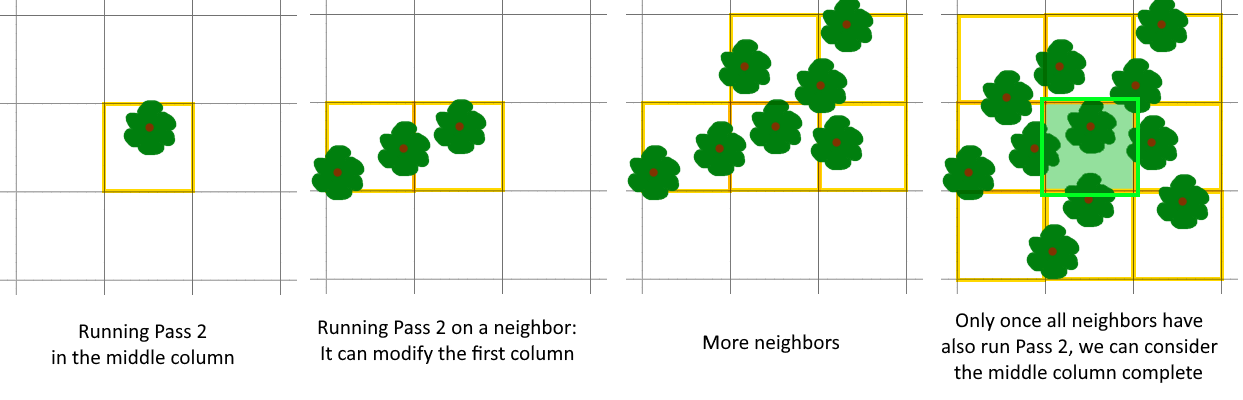
With 3 passes, even more columns have to be partially generated:
a a a a a a a a a a = pass 1 partially affected by b
a b b b b b b b a b = pass 2 incomplete, partially affected by itself
a b B B B B B b a B = pass 2 complete, partially affected by c
a b B c c c B b a c = pass 3 incomplete, partially affected by itself
a b B c C c B b a C = pass 3 complete
a b B c c c B b a
a b B B B B B b a
a b b b b b b b a
a a a a a a a a a
The generator does not do all this work from scratch everytime it needs to generate a column. Since columns will have to be re-accessed many times, they are cached in an internal map. Columns get unloaded when far enough from any viewer. This map can be previewed in the editor, when the terrain is present in the edited scene:
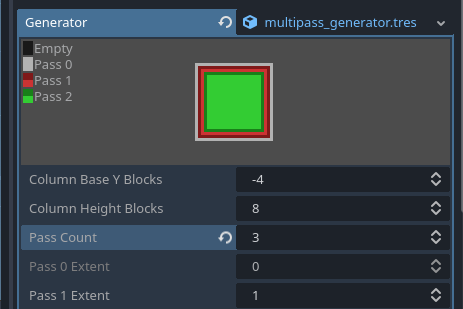
Each pass can be seen as concentric rectangular areas extending beyond the view distance of the viewer (note, you won't see those passes if your terrain has run_stream_in_editor disabled).
Passes that can access neighbors use two shades of color, where the brighter shade means all neighbors have run the same pass.
Determinism¶
A key feature of generators is to be deterministic. Generating the same column again must always give the same result, as long as parameters are the same (position, seed...). However, with multipass, a few factors can break determinism.
Column passes are executed in parallel, using multiple threads. Also, players can cause columns to generate from any direction. That means the order in which columns generate is unpredictable.
Consider neighbor columns A and B. A could generate a tree overlapping into B. But B can also generate a tree overlapping into A. As a result, if the neighbor tree has already been planted, you have to make sure not to erase parts of its trunk, or even leaves if they are different.
In this case:
- The result might no longer be deterministic, although you could decide it's ok if the differences are acceptable. In some cases results could be the same regardless of order.
- Structure generation can be bothered a bit, notably placement checks or trees growing through other structures. You might have to place voxels by choosing which voxel types or areas you can overwrite yourself.
Limitations¶
- This kind of generator only works with
VoxelTerrain, because it is very data-heavy: it is too expensive to run on the fly and directly produce LODs, like simpler single-pass generators can. If LOD has to be supported with a terrain using this generator, it will likely have to work differently and update slower, because it is required to generate the highest level of detail everywhere (i.e Distant Horizons mod in Minecraft). - It is generally more expensive than single-pass generators, and consumes more memory because it needs to cache partially-generated columns in a radius around every player, beyond their view distances. It does this to improve performance (which otherwise would be orders of magnitude worse). With a lot of passes or high extents, the amount of memory consumed by this cache could even exceed visible chunks.
- Column height is limited for practical reasons. Multipass cubic chunks were experimented with during development of
VoxelGeneratorMultipassCB, and they were significantly more expensive, and harder to work with in some cases, because of the inability to access a full vertical section (which would have to be infinite). - The reachable distance outside the main column is limited. It can be increased, but it gets expensive quickly. If you need to reach further to place very big structures spanning dozens of chunks across, you might have to think of a different approach. For example, generating a "blueprint" up-front (or deterministically), and rasterizing parts of it progressively when they intersect the column.
- The same instance of generator cannot be shared between multiple terrains. If you need the same generator on two terrains, make a copy.
- Implementation isn't ideal.
VoxelTerrainis very generic and works with infinite cubic chunks, while this generator needed different constraints to work well. As a result, there is some overhead that could be avoided if the terrain was entirely rewritten and dedicated to this kind of column structure. It wasn't done because it would become less configurable, break compatibility and take time to develop. - Currently, the column cache isn't saved, contrary to what was described in issue 545. So if the game restarts, some columns and their neighbors can be asked to generate again if blocks weren't saved in a
VoxelStream. This can be mitigated by saving generated blocks withVoxelStream.save_generator_output. In general, don't expectVoxelGeneratorto be called only once for a given chunk, because it might be called again in corner cases. Generators should be deterministic and not have race conditions.
Modifiers¶
Modifiers are generators that affect a limited region of the volume. They can stack on top of base generated voxels or other modifiers, and affect the final result. This is a workflow that mostly serves if your world has a finite size, and you want to set up specific shapes of the landscape in a non-destructive way from the editor.
Note
This feature is only implemented with VoxelLodTerrain at the moment, and only works to sculpt smooth voxels. It is in early stages so it is quite limited.
Modifiers can be added with nodes as child of the terrain. VoxelModifierSphere adds or subtracts a sphere, while VoxelModifierMesh adds or subtracts a mesh. For the latter, the mesh must be baked into an SDF volume first, using the VoxelMeshSDF resource.
Because modifiers are part of the procedural generation stack, destructive edits will always override them. If a block is edited, modifiers cannot affect it. It is then assumed that such edits would come from players at runtime, and that modifiers don't change.
Caching¶
Generators are designed to be deterministic: if the same area is generated twice, the result must be the same. This means, ultimately, we only need to store edited voxels (aka "destructive" editing), while non-edited regions can be recomputed on the fly. Even if you want to access one voxel and it happens to be in a non-edited location, then the generator will be called just to obtain that voxel.
However, if a generator is too expensive or not expected to run this way, it may be desirable to store the output in memory so that querying the same area again picks up the cached data.
By default, VoxelTerrain caches blocks in memory until they get far from any viewer. VoxelLodTerrain does not cache blocks by default. There is no option yet to change that behavior.
It is also possible to tell a VoxelGenerator to save its outputs to the current VoxelStream, if any is setup. However, these blocks will act as edited ones, so they will behave as if it was changes done destructively.